Megan Langford

Medial Triangles

Medial triangles are constructed first by taking the midpoints of each side on a triangle and then connecting them to form a smaller triangle inside the original one.

This builds on our last write-up as related to the centroid. If you recall, to construct the centroid, we first showed the medians of the triangle. The centroid is located where the medians intersect. If we take this one step further, we can also create a smaller triangle within the original one by simply connecting the midpoints of each side. As we do this, we can clearly see that the same point is actually the centroid for both triangles. This is because each of our medians is a perpendicular bisector of a side of the smaller triangle, and it also connects with the opposing vertex. This is precisely the construction we used to create the medians in the first place.

Our construction using Geometer’s Sketchpad appears to look like this:

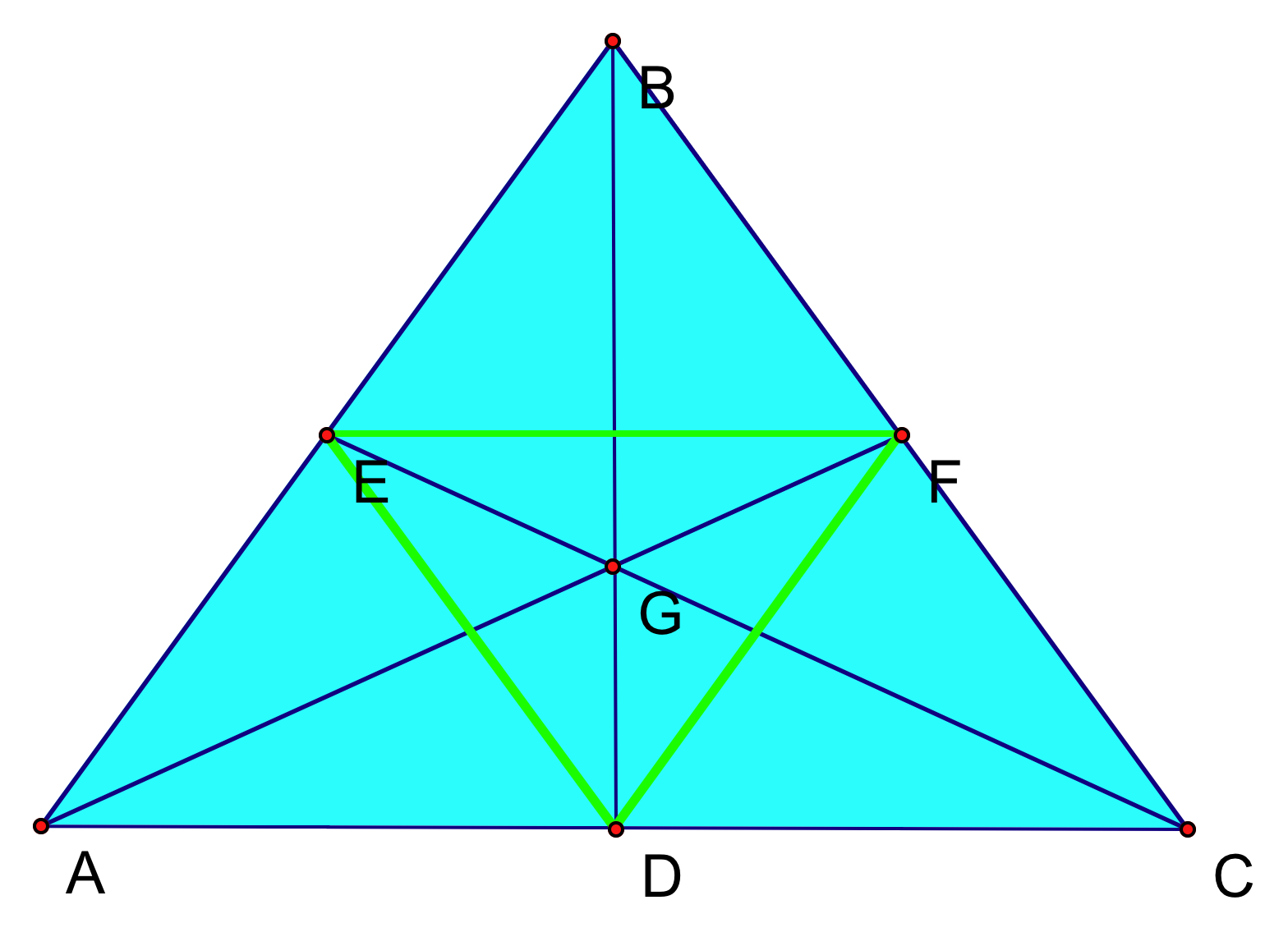
Our measurements for each of the sides are calculated using GSP:

We can first notice that both triangles appear to be roughly the same shape. So we will hypothesize that there could be a similarity relationship. In order to prove this, one method we can use is the SSS Similarity Theorem, which states that if there is a constant ratio between the corresponding side measurements of the 2 triangles, then the triangles are in fact similar. Our calculations would appear as follows:

Since these ratios are indeed constant, we know that the triangles are similar. In fact, we could also prove this similarity using the SAS or AA Similarity Theorems since we can easily calculate the necessary data using GSP.

Next, we can also notice that the medial triangle appears almost identical to each of the smaller triangles with which it shares a side. To prove that they are in fact identical, we can compare the side measurements. GSP measures them at:

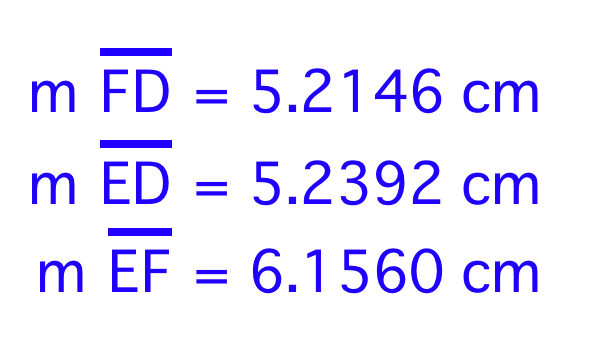
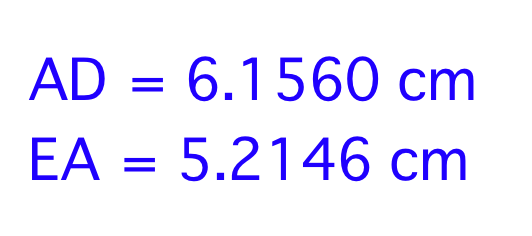
The two triangles share the side , so we know this has the same measurement. As for the other sides, we can see that has the same length as and has the same measurement as . Hence, these triangles are actually identical. Without loss of generality, we can apply the same analysis to the other 2 small triangles. Since the four of these triangles together form the total area of the large triangle, we can predict that the area of the medial triangle is one fourth of the total area of the large triangle. To check that this is true, we can use GSP to calculate the total area for both triangles. For the medial triangle, we are given an area of:

So if we are correct, then the area of the large triangle will be 13.0029452.0116 cm. As it turns out, GSP gives us:

So we now know that the medial triangle is indeed one fourth the area of the large triangle. For a hands-on exercise, we could also print out the shape and fold it into a pyramid. This would demonstrate our conclusion, since it would only work if each of these 4 smaller triangles were identical.

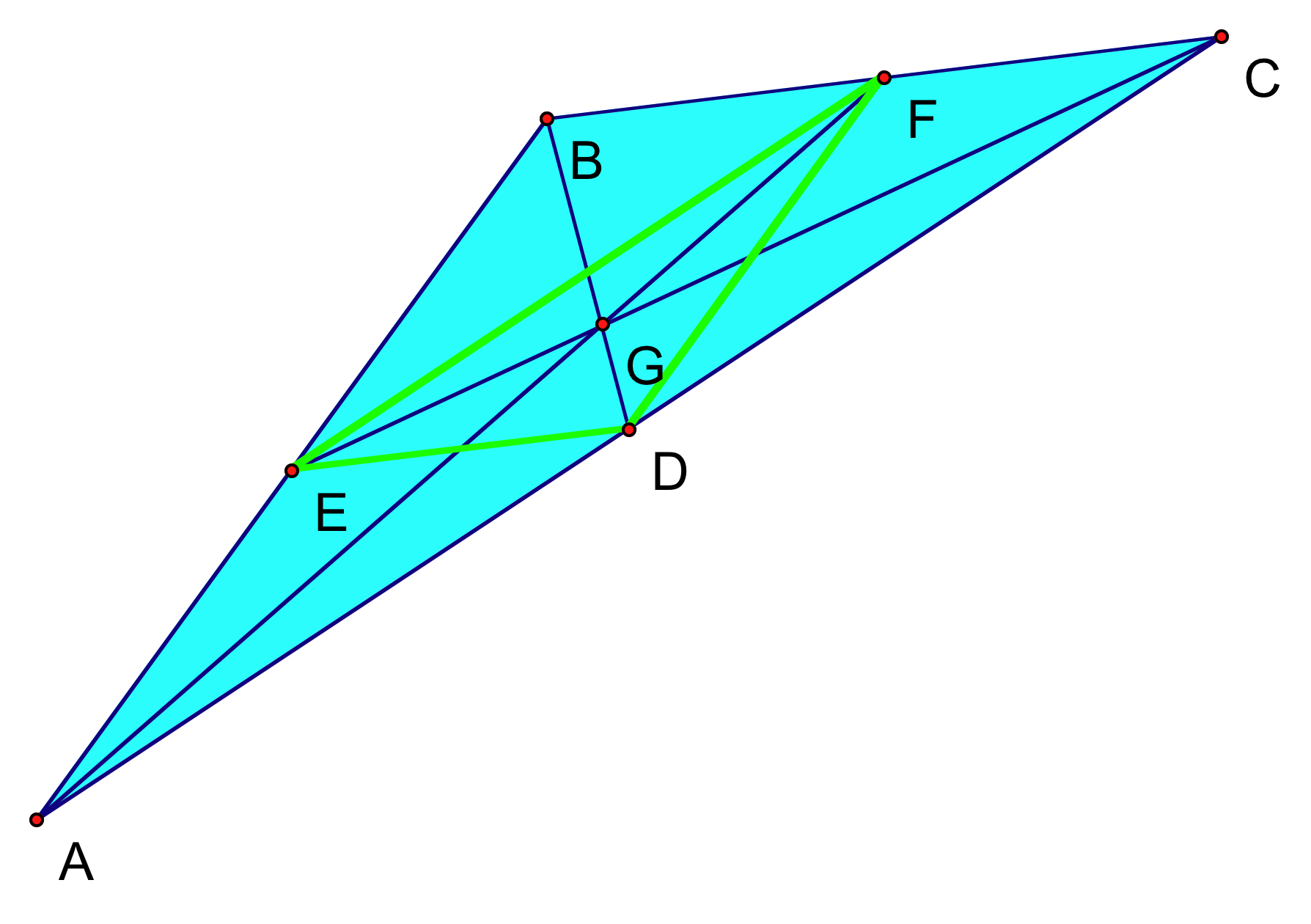
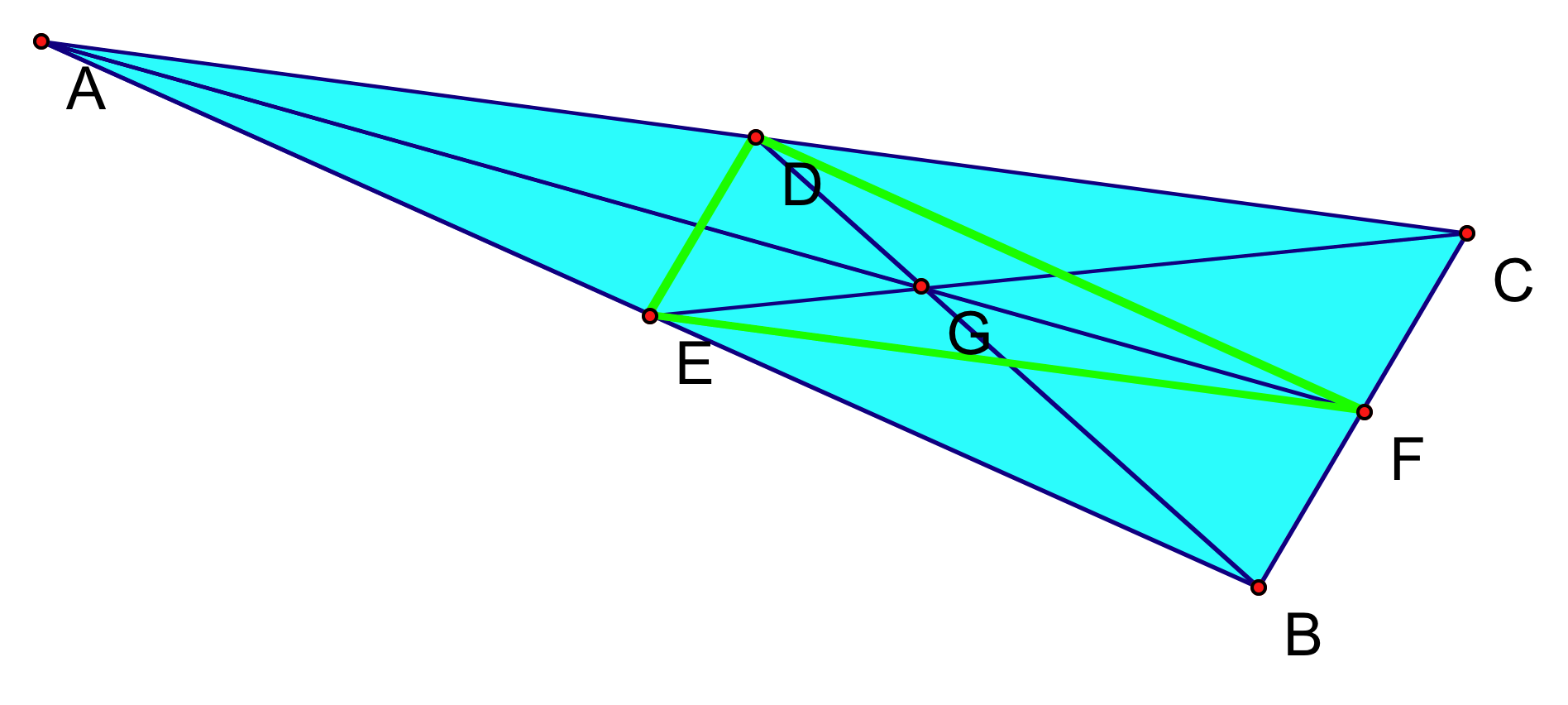
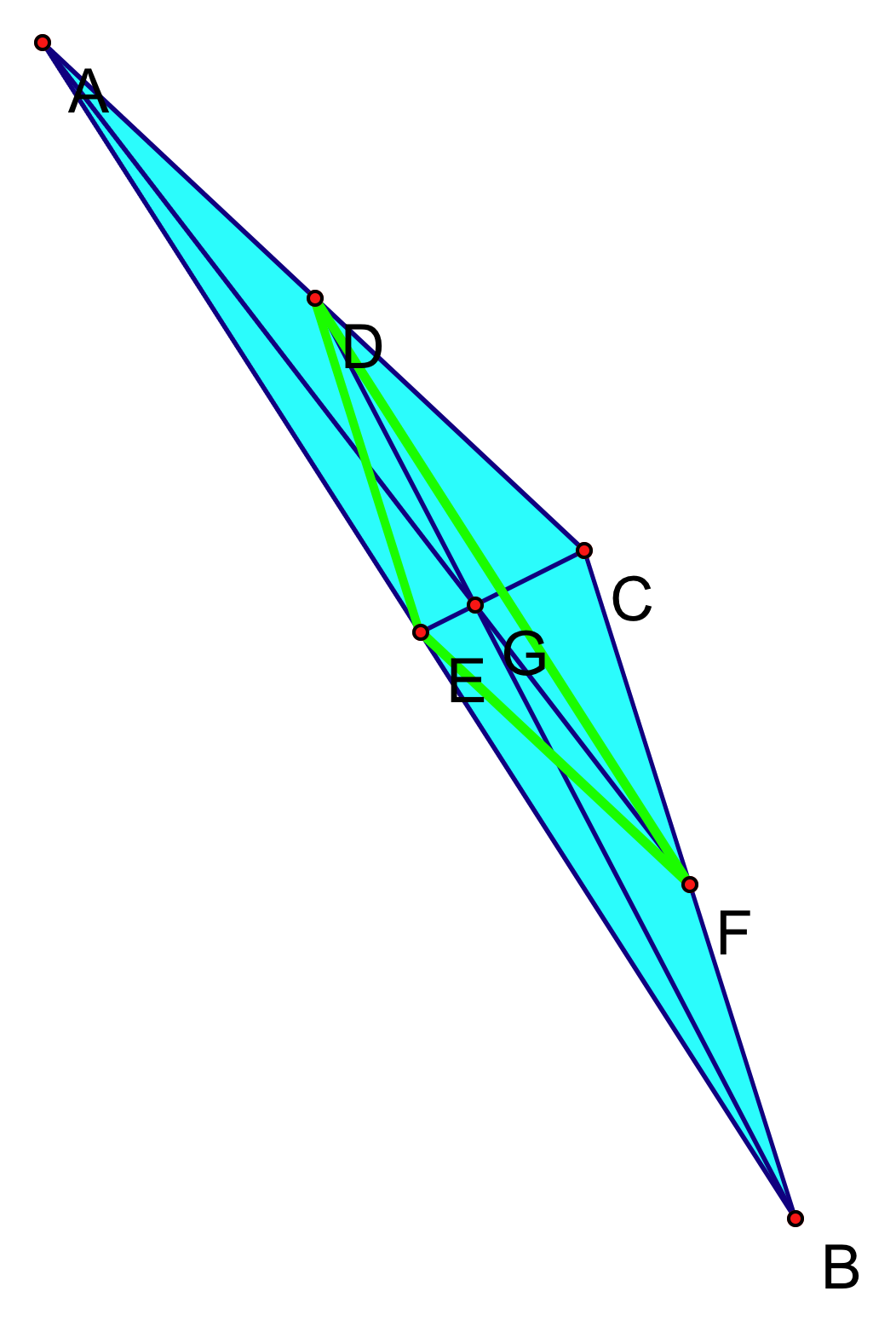
To show that this is true for all triangles, I will include images of several differently shaped triangles with their medial triangles inside. We can visually see the principle at work, or I will leave it to you to prove the relationship holds in a similar manner to our previous example.